Partition (number theory)
In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a composition. For example, 4 can be partitioned in five distinct ways:
- 4, 3 + 1, 2 + 2, 2 + 1 + 1, 1 + 1 + 1 + 1.
The order-dependent composition 1 + 3 is the same partition as 3 + 1, while 1 + 2 + 1 and 1 + 1 + 2 are the same partition as 2 + 1 + 1.
A summand in a partition is also called a part. The number of partitions of n is given by the partition function p(n). So p(4) = 5. The notation q ⊢ n means that q is a partition of n.
Partitions can be graphically visualized with Young diagrams or Ferrers diagrams. They occur in a number of branches of mathematics and physics, including the study of symmetric polynomials, the symmetric group and in group representation theory in general.
Contents |
Examples
The partitions of 4 are:
- 4
- 3 + 1
- 2 + 2
- 2 + 1 + 1
- 1 + 1 + 1 + 1
In some sources partitions are treated as the sequence of summands, rather than as an expression with plus signs. For example, the partition 2 + 1 + 1 might instead be written as the tuple (2, 1, 1) or in the even more compact form (2, 12) where the superscript indicates the number of repetitions of a term.
Restricted partitions
Among the 22 partitions for the number 8, 6 contain only odd parts:
- 7 + 1
- 5 + 3
- 5 + 1 + 1 + 1
- 3 + 3 + 1 + 1
- 3 + 1 + 1 + 1 + 1 + 1
- 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
If we count the partitions of 8 with distinct parts, we also obtain the number 6:
- 8
- 7 + 1
- 6 + 2
- 5 + 3
- 5 + 2 + 1
- 4 + 3 + 1
It is true for all positive numbers that the number of partitions with odd parts always equals the number of partitions with distinct parts. This result was proved by Leonhard Euler in 1748[1] and is a special case of Glaisher's theorem.
Some similar results about restricted partitions can be obtained by the aid of a visual tool, a Ferrers graph (also called Ferrers diagram, since it is not a graph in the graph-theoretical sense, or sometimes Young diagram, alluding to the Young tableau).
Partition function
In number theory, the partition function p(n) represents the number of possible partitions of a natural number n, which is to say the number of distinct (and order independent) ways of representing n as a sum of natural numbers. By convention p(0) = 1, p(n) = 0 for n negative.
The first few values of the partition function are (starting with p(0)=1):
- 1, 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, … (sequence A000041 in OEIS).
The value of p(n) has been computed for large values of n, for example p(100)=190,569,292 and p(1000) is approximately 2.4×1031.[2]
As of November 2011[update], the largest known prime number that counts a number of partitions is p(80036992), with 9958 decimal digits, found by Bernardo Boncompagni.[3]
For every type of restricted partition there is a corresponding function for the number of partitions satisfying the given restriction. An important example is q(n)=the number of partitions of n into distinct parts.[4] As noted above, q(n) is also the number of partition of n into only odd parts. The first few values of the q(n) are (starting with q(0)=1):
- 1, 1, 1, 2, 2, 3, 4, 5, 6, 8, 10, … (sequence A000009 in OEIS).
Intermediate function
One way of getting a handle on the partition function involves an intermediate function p(k, n), which represents the number of partitions of n using only natural numbers at least as large as k. For any given value of k, partitions counted by p(k, n) fit into exactly one of the following categories:
- smallest addend is k
- smallest addend is strictly greater than k.
The number of partitions meeting the first condition is p(k, n − k). To see this, imagine a list of all the partitions of the number n − k into numbers of size at least k, then imagine appending "+ k" to each partition in the list. Now what is it a list of? As a side note, one can use this to define a sort of recursion relation for the partition function in terms of the intermediate function, namely
where 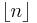 is the floor function.
is the floor function.
The number of partitions meeting the second condition is p(k + 1, n) since a partition into parts of at least k that contains no parts of exactly k must have all parts at least k + 1.
Since the two conditions are mutually exclusive, the number of partitions meeting either condition is p(k + 1, n) + p(k, n − k). The recursively defined function is thus:
- p(k, n) = 0 if k > n
- p(k, n) = 1 if k = n
- p(k, n) = p(k+1, n) + p(k, n − k) otherwise.
This function tends to exhibit deceptive behavior.
- p(1, 4) = 5
- p(2, 8) = 7
- p(3, 12) = 9
- p(4, 16) = 11
- p(5, 20) = 13
- p(6, 24) = 16
Our original function p(n) is just p(1, n).
The values of this function:
-
k 1 2 3 4 5 6 7 8 9 10 n 1 1 0 0 0 0 0 0 0 0 0 2 2 1 0 0 0 0 0 0 0 0 3 3 1 1 0 0 0 0 0 0 0 4 5 2 1 1 0 0 0 0 0 0 5 7 2 1 1 1 0 0 0 0 0 6 11 4 2 1 1 1 0 0 0 0 7 15 4 2 1 1 1 1 0 0 0 8 22 7 3 2 1 1 1 1 0 0 9 30 8 4 2 1 1 1 1 1 0 10 42 12 5 3 2 1 1 1 1 1
Generating function
The generating function for p(n) is given by:[5]
Expanding each term on the right-hand side as a geometric series, we can rewrite it as
- (1 + x + x2 + x3 + ...)(1 + x2 + x4 + x6 + ...)(1 + x3 + x6 + x9 + ...) ....
The xn term in this product counts the number of ways to write
- n = a1 + 2a2 + 3a3 + ... = (1 + 1 + ... + 1) + (2 + 2 + ... + 2) + (3 + 3 + ... + 3) + ...,
where each number i appears ai times. This is precisely the definition of a partition of n, so our product is the desired generating function. More generally, the generating function for the partitions of n into numbers from a set A can be found by taking only those terms in the product where k is an element of A. This result is due to Euler.
The formulation of Euler's generating function is a special case of a q-Pochhammer symbol and is similar to the product formulation of many modular forms, and specifically the Dedekind eta function.
The denominator of the product is Euler's function and can be written, by the pentagonal number theorem, as
where the exponents of x on the right hand side are the generalized pentagonal numbers; i.e., numbers of the form ½m(3m − 1), where m is an integer. The signs in the summation alternate as (-1)m. This theorem can be used to derive a recurrence for the partition function:
- p(k) = p(k − 1) + p(k − 2) − p(k − 5) − p(k − 7) + p(k − 12) + p(k − 15) − p(k − 22) − ...
where p(0) is taken to equal 1, and p(k) is taken to be zero for negative k.
Another way of stating this is that the value of p(n) can be found from the formula[6]
I.e., p(n) is the determinant of the n×n truncation of the infinite-dimensional Toeplitz matrix shown above. The only non-zero diagonals of this matrix are those which start on a row labeled by a generalized pentagonal number qm. (The superdiagonal is taken to start on row "0".) On these diagonals, the matrix element is (-1)m+1. This follows from a general formula for the quotients for power series.[7]
The generating function for q(n) is given by:[8]
The second product can be written ϕ(x2) / ϕ(x) where ϕ is Euler's function; the pentagonal number theorem can be applied to this as well giving a recurrence for q:[9]
- q(k) = ak+q(k − 1) + q(k − 2) − q(k − 5) − q(k − 7) + q(k − 12) + q(k − 15) − q(k − 22) − ...
where ak is (−1)m if k =3m2-m for some integer m and is 0 otherwise.
The determinant formula for the quotient of power series can be applied to the expression ϕ(x2) / ϕ(x) to produce the expression
where the diagonals in the first n columns are constants equal to the coefficients in the power series for ϕ(x) and the last column has values ak given above.
Gaussian binomial coefficient
The Gaussian binomial coefficient is related to integer partitions. The Gaussian binomial coefficient is defined as:
The number of integer partitions that would fit into a k by l rectangle (when expressed as a Ferrers or Young diagram) is denoted by p(n, k, l). The Gaussian binomial coefficient is related to the generating function of p(n, k, l) by the following equality:
Restricted partition generating functions
The generating function can be adapted to describe restricted partitions. For example, the generating function for integer partitions into distinct parts is:
and the generating function for partitions consisting of particular summands (specified by a set T of natural numbers) is:
This can be used to solve Change-making problems (where the set T specifies the available coins). Generating functions can be used to proof various identities involving integer partitions quite easily, for example the one mentioned in the Restricted partitions section. The generating function for partitions into odd summands is:
which is the generating function for partitions into distinct summands.
Congruences
Srinivasa Ramanujan is credited with discovering that "congruences" in the number of partitions exist for integers ending in 4 and 9.
For instance, the number of partitions for the integer 4 is 5. For the integer 9, the number of partitions is 30; for 14 there are 135 partitions. This is implied by an identity, also by Ramanujan,[10]
where the series 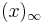 is defined as
is defined as
He also discovered congruences related to 7 and 11:
Since 5, 7, and 11 are consecutive primes, one might think that there would be such a congruence for the next prime 13, 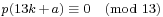 for some a. This is, however, false. It can also be shown that there is no congruence of the form
for some a. This is, however, false. It can also be shown that there is no congruence of the form 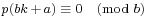 for any prime b other than 5, 7, or 11.
for any prime b other than 5, 7, or 11.
In the 1960s, A. O. L. Atkin of the University of Illinois at Chicago discovered additional congruences for small prime moduli. For example:
In 2000, Ken Ono of the University of Wisconsin–Madison proved that there are such congruences for every prime modulus. A few years later Ono, together with Scott Ahlgren of the University of Illinois, proved that there are partition congruences modulo every integer coprime to 6.[11]
Partition function formulas
An asymptotic expression for p(n) is given by
This asymptotic formula was first obtained by G. H. Hardy and Ramanujan in 1918 and independently by J. V. Uspensky in 1920. Considering p(1000), the asymptotic formula gives about 2.4402 × 1031, reasonably close to the exact answer given above (1.415% larger than the true value).
In 1937, Hans Rademacher was able to improve on Hardy and Ramanujan's results by providing a convergent series expression for p(n). It is
where
It can be shown that the derivative part of the sum can be simplified. [12] Here, the notation (m, n) = 1 implies that the sum should occur only over the values of m that are relatively prime to n. The function s(m, k) is a Dedekind sum. The proof of Rademacher's formula involves Ford circles, Farey sequences, modular symmetry and the Dedekind eta function in a central way.
In January 2011, it was announced that Ono and Jan Hendrik Bruinier, of the Technische Universität Darmstadt, had developed a finite, algebraic formula determining the value of p(n) for any positive integer n.[13] [14]
Ferrers diagram
The partition 6 + 4 + 3 + 1 of the positive number 14 can be represented by the following diagram; these diagrams are named in honor of Norman Macleod Ferrers:
| 6 + 4 + 3 + 1 |
The 14 circles are lined up in 4 columns, each having the size of a part of the partition. The diagrams for the 5 partitions of the number 4 are listed below:
| 4 | = | 3 + 1 | = | 2 + 2 | = | 2 + 1 + 1 | = | 1 + 1 + 1 + 1 |
If we now flip the diagram of the partition 6 + 4 + 3 + 1 along its main diagonal, we obtain another partition of 14:
| ↔ | ||
| 6 + 4 + 3 + 1 | = | 4 + 3 + 3 + 2 + 1 + 1 |
By turning the rows into columns, we obtain the partition 4 + 3 + 3 + 2 + 1 + 1 of the number 14. Such partitions are said to be conjugate of one another. In the case of the number 4, partitions 4 and 1 + 1 + 1 + 1 are conjugate pairs, and partitions 3 + 1 and 2 + 1 + 1 are conjugate of each other. Of particular interest is the partition 2 + 2, which has itself as conjugate. Such a partition is said to be self-conjugate.
Claim: The number of self-conjugate partitions is the same as the number of partitions with distinct odd parts.
Proof (outline): The crucial observation is that every odd part can be "folded" in the middle to form a self-conjugate diagram:
| ↔ |
One can then obtain a bijection between the set of partitions with distinct odd parts and the set of self-conjugate partitions, as illustrated by the following example:
| ↔ | ||
| 9 + 7 + 3 | = | 5 + 5 + 4 + 3 + 2 |
| Dist. odd | self-conjugate |
Similar techniques can be employed to establish, for example, the following equalities:
- The number of partitions of n into no more than k parts is the same as the number of partitions of n into parts no larger than k.
- The number of partitions of n into no more than k parts is the same as the number of partitions of n + k into exactly k parts.
Young diagrams
An alternative visual representation of an integer partition is its Young diagram, named after the British mathematician Alfred Young. Rather than representing a partition with dots, as in the Ferrers diagram, the Young diagram uses boxes. Thus, the Young diagram for the partition 5 + 4 + 1 is
while the Ferrers diagram for the same partition is
While this seemingly trivial variation doesn't appear worthy of separate mention, Young diagrams turn out to be extremely useful in the study of symmetric functions and group representation theory: in particular, filling the boxes of Young diagrams with numbers (or sometimes more complicated objects) obeying various rules leads to a family of objects called Young tableaux, and these tableaux have combinatorial and representation-theoretic significance.
See also
- Young's lattice
- Dominance order
- Partition of a set
- Plane partition
- Polite number, defined by partitions into consecutive integers
- Multiplicative partition
- Twelvefold way
- Ewens's sampling formula
- Faà di Bruno's formula
- Multiset
- Newton's identities
- Leibniz's distribution table for integer partitions
- Durfee square
- Smallest-parts function
- A Goldbach partition is the partition of an even number into primes (see Goldbach's conjecture)
Notes
- ^ Andrews, George E. Number Theory. W. B. Saunders Company, Philadelphia, 1971. Dover edition, page 149–150.
- ^ Sloane's A070177 . The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ http://primes.utm.edu/top20/page.php?id=54
- ^ Notation follows Abramowitz and Stegun p. 825
- ^ Abramowitz and Stegun p. 825, 24.2.1 eq. I(B)
- ^ J. Malenfant, "Finite, Closed-form Expressions for the Partition Function and for Euler, Bernoulli, and Stirling Numbers"
- ^ The formula, due to Henri Faure, can be found in: Muir, Thomas (1920). The Theory of Determinants in the Historical Order of Development. II. Macmillan and Co.. p. 212. http://quod.lib.umich.edu/u/umhistmath/acm9350.0002.001/229.
- ^ Abramowitz and Stegun p. 825, 24.2.2 eq. I(B)
- ^ Abramowitz and Stegun p. 826, 24.2.2 eq. II(A)
- ^ Berndt and Ono, "Ramanujan's Unpublished Manuscript on the Partition and Tau Functions with Proofs and Commentary" [1]
- ^ Ono, Ken; Ahlgren, Scott (2001). "Congruence properties for the partition function". Proceedings of the National Academy of Sciences 98 (23): 12,882–12,884. doi:10.1073/pnas.191488598. http://www.math.wisc.edu/~ono/reprints/061.pdf.
- ^ "WolframAlpha". http://www.wolframalpha.com/input/?i=d%2Fdn+%28%281%2Fsqrt%28n-%281%2F24%29%29%29*sinh%28pi%2Fk*sqrt%28%282%2F3%29*%28n-%281%2F24%29%29%29%29%29.
- ^ http://www.aimath.org/news/partition/
- ^ Bruinier and Ono, "Algebraic formulas for the coefficients of half-integral weight harmonic weak Maass forms"
References
- George E. Andrews, The Theory of Partitions (1976), Cambridge University Press. ISBN 0-521-63766-X .
- Tom M. Apostol, Modular functions and Dirichlet Series in Number Theory (1990), Springer-Verlag, New York. ISBN 0-387-97127-0 (See chapter 5 for a modern pedagogical intro to Rademacher's formula).
- Sautoy, Marcus Du. The Music of the Primes. New York: Perennial-HarperCollins, 2003.
- Lehmer, D. H. (1939). "On the remainder and convergence of the series for the partition function". Trans. Amer. Math. Soc. 46: 362–373. doi:10.1090/S0002-9947-1939-0000410-9. MR0000410. Provides the main formula (no derivatives), remainder, and older form for Ak(n).)
- Gupta, Gwyther, Miller, Roy. Soc. Math. Tables, vol 4, Tables of partitions, (1962) (Has text, nearly complete bibliography, but they (and Abramowitz) missed the Selberg formula for Ak(n), which is in Whiteman.)
- Ian G. Macdonald, Symmetric functions and Hall polynomials, Oxford University Press, 1979, ISBN 0-19-853530-9 (See section I.1)
- Ken Ono, Distribution of the partition function modulo m, Annals of Mathematics 151 (2000) pp 293–307. (This paper proves congruences modulo every prime greater than 3)
- Richard P. Stanley, Enumerative Combinatorics, Volumes 1 and 2. Cambridge University Press, 1999 ISBN 0-521-56069-1
- A. L. Whiteman, A sum connected with the series for the partition function, Pacific Journal of Math. 6:1 (1956) 159–176. (Provides the Selberg formula. The older form is the finite Fourier expansion of Selberg.)
- Hans Rademacher, Collected Papers of Hans Rademacher, (1974) MIT Press; v II, p 100–107, 108–122, 460–475.
- Miklós Bóna (2002). A Walk Through Combinatorics: An Introduction to Enumeration and Graph Theory. World Scientific Publishing. ISBN 981-02-4900-4. (qn elementary introduction to the topic of integer partition, including a discussion of Ferrers graphs)
- George E. Andrews, Kimmo Eriksson (2004). Integer Partitions. Cambridge University Press. ISBN 0-521-60090-1.
- 'A Disappearing Number', devised piece by Complicite, mention Ramanujan's work on the Partition Function, 2007
External links
- Partition and composition calculator
- First 4096 values of the partition function
- An algorithm to compute the partition function
- Weisstein, Eric W., "Partition" from MathWorld.
- Weisstein, Eric W., "Partition Function P" from MathWorld.
- Pieces of Number from Science News Online
- Lectures on Integer Partitions by Herbert S. Wilf
- Counting with partitions with reference tables to the On-Line Encyclopedia of Integer Sequences
- Integer::Partition Perl module from CPAN
- Fast Algorithms For Generating Integer Partitions
- Generating All Partitions: A Comparison Of Two Encodings
- Amanda Folsom, Zachary A. Kent, and Ken Ono, l-adic properties of the partition function. In press.
- Jan Hendrik Bruinier and Ken Ono, An algebraic formula for the partition function. In press.
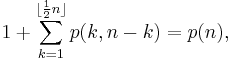
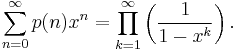
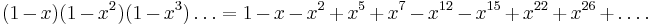
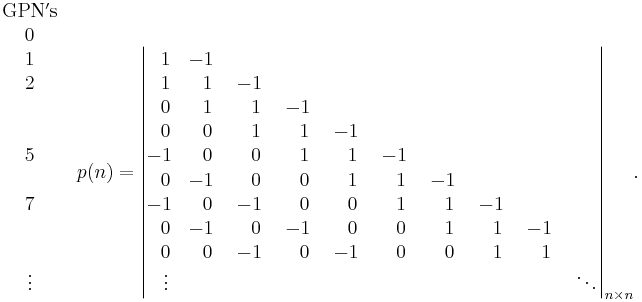
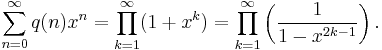
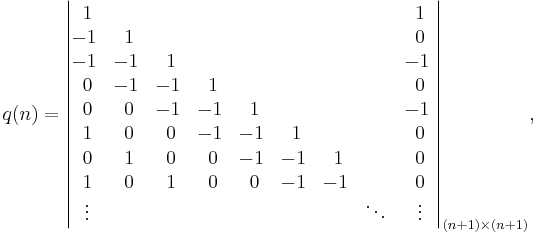
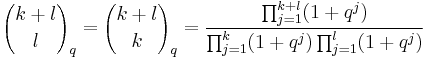
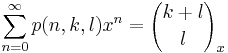
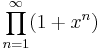
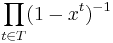
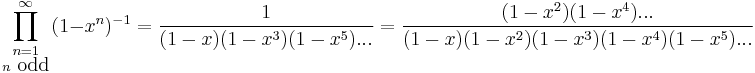
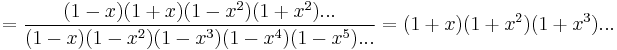
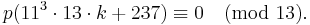
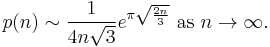
![p(n)=\frac{1}{\pi \sqrt{2}} \sum_{k=1}^\infty \sqrt{k}\, A_k(n)\,
\frac{d}{dn} \left(
\frac {1} {\sqrt{n-\frac{1}{24}}}
\sinh \left[ \frac{\pi}{k}
\sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)}\right]
\right)](/2012-wikipedia_en_all_nopic_01_2012/I/a6f5a93fa66e5fb59a4e988998d43a9d.png)
![A_k(n) = \sum_{0 \,\le\, m \,<\, k; \; (m,\, k) \,=\, 1}
e^{ \pi i \left[ s(m,\, k) \;-\; \frac{1}{k} 2 nm \right] }.](/2012-wikipedia_en_all_nopic_01_2012/I/15bef4db1dce13351660c67f8059e8fa.png)